351. Android Unlock Patterns

Given an Android3x3key lock screen and two integersmandn, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum ofmkeys and maximumnkeys.

Rules for a valid pattern:

1. Each pattern must connect at least m keys and at most n keys.
2. All the keys must be distinct.
3. If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
4. The order of keys used matters.

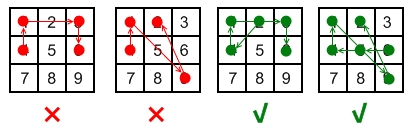
Explanation:

| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |

Invalid move:4 - 1 - 3 - 6
Line 1 - 3 passes through key 2 which had not been selected in the pattern.

Invalid move:4 - 1 - 9 - 2
Line 1 - 9 passes through key 5 which had not been selected in the pattern.

Valid move:2 - 4 - 1 - 3 - 6
Line 1 - 3 is valid because it passes through key 2, which had been selected in the pattern

Valid move:6 - 5 - 4 - 1 - 9 - 2
Line 1 - 9 is valid because it passes through key 5, which had been selected in the pattern.

Example:
Given m= 1,n= 1, return 9.

S1： backtracking

如果没有不能穿过的条件限制，实际上就是求1-9其中n-m个数的permutation，用backtracking递归即可。加上了不能穿过的要求就是多一个条件限制

通过上一个key和当前key的坐标来判断他们的连线是否穿过某一key: 若两key x,y坐标之和(x1+x2),(y1+y2)都为偶数则穿过key, 通过visited map判断该key是否被访问过。

利用键盘的对称性减少recursion的次数（1,3,7,9）一样，（2，4，6，8）一样

class Solution {
public:
    int numberOfPatterns(int m, int n) {
        int count = 0;
        for (int i = m; i <= n; ++i) {           
            vector<bool> visited(9, false);
            count += 4 * dfs(i - 1, 0, visited);
            count += 4 * dfs(i - 1, 1, visited);            
            count += dfs(i - 1, 4, visited);
        }
        return count;
    }
private:    
    int dfs(int n, int last, vector<bool>& visited) {
        if (n == 0) return 1;
        visited[last] = true;
        int result = 0;
        for (int i = 0; i < 9; ++i) {
            if (!visited[i] && isValid (last, i, visited)) {
                visited[i] = true;
                result += dfs(n - 1, i, visited);
                visited[i] = false;
            }
        }
        visited[last] = false;
        return result;
    }

    bool isValid(int num1, int num2, vector<bool>& visited) {
        int x1 = num1 / 3, y1 = num1 % 3, x2 = num2 / 3, y2 = num2 % 3;
        int x = x1 + x2, y = y1 + y2;
        return (x & 1 || y & 1) || visited[(x / 2) * 3 + y / 2];
    }
};