https://www.youtube.com/watch?v=CWDQJGaN1gY

http://www.geeksforgeeks.org/binary-indexed-tree-or-fenwick-tree-2/

The idea is based on the fact that all positive integers can be represented as sum of powers of 2. For example 19 can be represented as 16 + 2 + 1. Every node of BI Tree stores sum of n elements where n is a power of 2.

For example,

1 = [0] + 2^0, 1st node store sum of elements 0-0, 1 element
2 = [0] + 2^1, 2nd node store sum of elements 0-1, 2 elements
3 = [2^1] + 2^0, 3rd node store sum of elements 2-2, 1 element
7 = [2^2 + 2^1] + 2^0, 7th node store sum of elements 6-6, 1 element

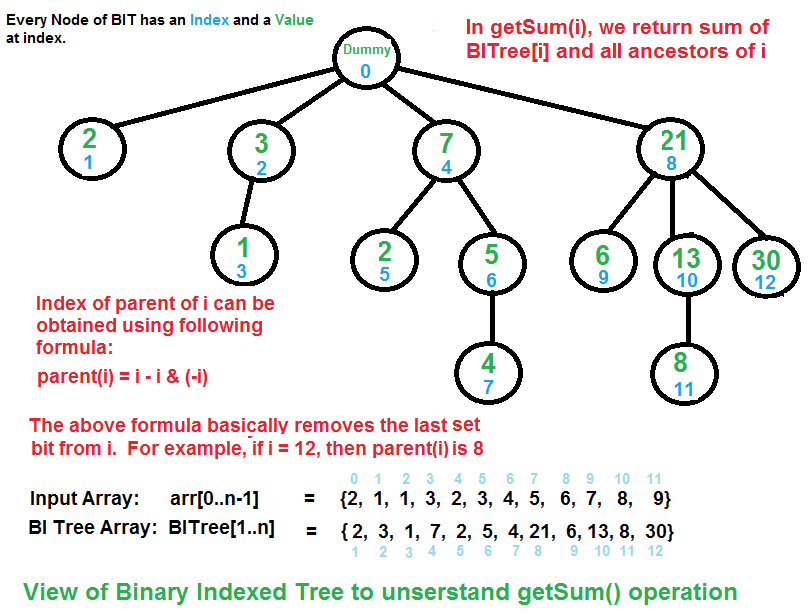
Trace parent by minus the least significant 1, trace child by add the least significant 1. (x&(-x) isolate the right most 1-bit )

1. We first get 2’s complement by negating it and obtain “-index”, which has binary representation 11110100.
2. Then we binary-and “&” with “index” and obtain “index & (-index)”, which is 00001100 & 11110100 = 00000100.
3. Subtract the result of step 2 from “index” and obtain “index -= index & (-index)”, which is 00001000

index -= index & (-index) go to parent, index += index & (-index) go to child